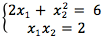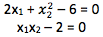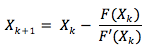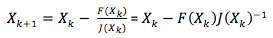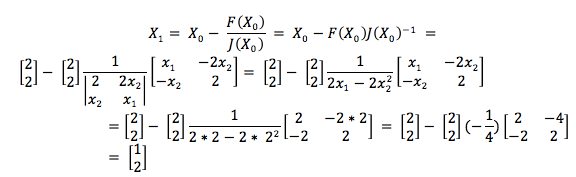Rozwiązywanie układu równań nieliniowych metodą Newtona
Załóżmy, że mamy do rozwiązania układ równań nieliniowych czyli taki, który przybiera postać f(x) = 0 lub g(x) = h(x). Cały problem polega jednak na tym, że nasz układ jest tak duży iż rozwiązanie go „metodą tradycyjną” przy użyciu kartki i długopisu nie wchodzi w grę. Trzeba więc do tego celu skorzystać z dobrodziejstw techniki czyli komputera. I tutaj zaczynają się kolejne schody…
Jak pewnie większości z Was obiło się o uszy, przy tego typu problemach nie możemy tak po prostu nakazać komputerowi wykonać konkretne obliczenia i czekać na wynik, gdyż albo w ogóle go nie dostaniemy (bo algorytm będzie wykonywał się przez kilkanaście lat) albo będzie on niepoprawny. Nie ma jednak się czym załamywać bowiem już jakiś czas temu kilku mądrych ludzi opracowało stosowne metody numeryczne, które pomogą nam rozwiązać niniejszy problem.
Należy jednak przy tym pamiętać, że równanie nieliniowe charakteryzuje się tym, że może nie mieć żadnego rozwiązania lub też może mieć ich wiele. Nie możemy więc tak po prostu zastosować znanej wszystkim metody Newtona. Będziemy musieli wprowadzić tutaj pewne modyfikacje. Różnica bowiem polega na tym, że w tym przypadku działamy na zmiennych macierzowych, a zamiast pochodnej liczymy jakobian macierzy.
Przeanalizujmy to na przykładzie…
Mamy dany następujący układ równań:
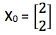
Do dalszych rozważań przyjmujemy punkt startowy:
Po przekształceniu równań otrzymujemy następującą postać:
Dostajemy więc układ równań nieliniowych:
Kolejnym krokiem będzie obliczenie wcześniej wspomnianego jakobianu macierzy (w przypadku równań liniowych liczylibyśmy pochodne):
Wzór ogólny:
Przykład:
Dalej postępujemy analogicznie jak w „tradycyjnej” wersji metody Newtona:
Dla przypomnienia w metodzie Newtona kolejne przybliżenia dane są wzorem rekurencyjnym:
W naszym przypadku będzie to tak:
Wzór ogólny:
Przykład:
1 iteracja:
2 iteracja:
Drugą iterację i każdą kolejną wykonujemy analogicznie z tym wyjątkiem, że startujemy od „nowego” wektora uzyskanego w iteracji poprzedniej. Czyli w naszym przypadku będzie to wektor:
Iteracje kontynuujemy do momentu uzyskania satysfakcjonującej dokładności.