Minimalna liczba nawiasów przy przekształcaniu wyrażeń z „Odwrotnej Notacji Polskiej” (ONP)

Algorytm minimalnej liczby nawiasów przy konwersji z ONP do INF

Problem minimalnej liczby nawiasów nie jest wbrew pozorom tak bardzo skomplikowany jak by się mogło wydawać. Aby go rozwiązać będziemy potrzebowali przede wszystkim jakieś funkcji, która zwracała by nam informację o priorytecie danego działania arytmetycznego zgodnie z kolejnością wykonywania działań:

Znając już priorytety poszczególnych działań arytmetycznych możemy zastanowić się nad tym w jaki sposób wykorzystać te informacje do zapisania minimalnej liczby nawiasów.

Mając wyrażenie:

ab+cd*/

Można go zapisać w postaci drzewa:

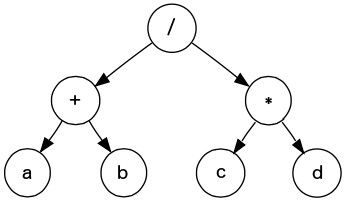
Przy minimalnej liczbie nawiasów, po poprawnej konwersji do postaci infiksowej otrzymamy taki wynik:

(a+b)/(c*d)

Jak widać w nawias zostało wzięte dodawanie (+) oraz mnożenie (*).

Przy decydowaniu, które wyrażenie ma zostać wzięte w nawias należy kierować się poniższymi regułami:

• gdy priorytet operatora w korzeniu poddrzewa jest większy od priorytetu operatora w lewym potomku to podwyrażenie z lewego potomka bierzemy w nawias,
• gdy priorytet operatora w korzeniu poddrzewa jest większy lub równy od priorytetu operatora z prawego potomka to podwyrażenie znajdujące się w prawym potomku bierzemy w nawias.

Zgodnie z tymi regułami mamy w korzeniu lewego poddrzewa operator dodawania (+), którego priorytet zgodnie z tabelką wyżej wynosi 1, w lewym potomku (lewym dziecku) mamy natomiast cyfrę oznaczoną w tym przykładzie literą „a” czyli priorytet wynosi 5. Tak więc mamy priorytet w korzeniu poddrzewa mniejszy niż priorytet w lewym dziecku, więc nic nie robimy.

Przejdźmy teraz do prawego potomka. Tam również mamy cyfrę (w tym przykładzie zapisaną jako literę) więc analogicznie jak wyżej, nic nie robimy bo 1 jest mniejsze od 5.

Drugi przypadek, w prawym poddrzewie priorytet korzenia wynosi 2 (operator mnożenia (*)) ważne jest jednak to, że zarówno w lewym oraz prawym dziecku mamy cyfrę (w tym przykładzie zapisaną jako literę) czyli priorytet wynosi 5. No i znowu analogicznie 2 jest mniejsze od 5 więc nic nie robimy.

Przechodzimy teraz wyżej. Mamy w korzeniu poddrzewa dzielenie (/) czyli priorytet będzie wynosił 2. Lewy potomek to dodawanie z priorytetem 1. Tak więc priorytet z korzenia jest większy od priorytetu lewego dziecka. Zgodnie z powyższymi punktami (pierwszy punkt) wyrażenie z lewego potomka bierzemy w nawias czyli a+b ma być w nawiasie.

Po prawej stronie mamy dziecko, którego priorytetem jest 2 (dla dzielenia: /), a w korzeniu mamy mnożenie i też mamy priorytet 2. No i znowu zgodnie z drugim puntem, priorytet korzenia jest równy priorytetowi prawego dziecka więc wyrażenie c*d bierzemy w nawias.

Strony: 1 2 3 4

Algorytmy, INF, minimalna liczba nawiasów, Minimalna liczba nawiasów przy konwersji z ONP, Odwrotna Notacja Polska, ONP, Programowanie, Reverse Polish notation