Abstrakcyjne struktury danych: Drzewa BST – porządki przeglądania
Drzewo przeszukiwań binarnych (ang. Binary Search Tree (BST)) to jedna z popularniejszych struktur danych, która przy dobrej organizacji (zrównoważonym drzewie) pozwala odnaleźć konkretny element w pesymistycznym czasie rzędu log(n). Do tematyki równoważenia drzewa jeszcze wrócę w innym artykule, a dzisiaj chciałem natomiast opisać czym w ogóle jest drzewo BST oraz jego porządki przeglądania.
Zacznijmy może od definicji drzewa BST – w skrócie jest to dynamiczna struktura danych będąca drzewem, w której lewe poddrzewo każdego węzła zawiera wyłącznie elementy o kluczach mniejszych niż klucz węzła, a prawe poddrzewo zawiera wyłącznie elementy o kluczach nie mniejszych niż klucz węzła. Warto również dodać, że węzły oprócz klucza, przechowują również wskaźniki na swojego prawego i lewego syna oraz ojca.
Skoro znamy już definicję drzewa BST to pora omówić trzy sposoby rekursywnego przejścia po elementach z takiej struktury danych:
- Pre-order – „przejście wzdłużne”,
- In-order – „przejście poprzeczne”,
- Post-order – „przejście wsteczne”.
Najłatwiej będzie to chyba omówić na przykładzie:
Pre-order
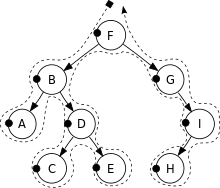
Idea polega tutaj na przechodzeniu w pierwszej kolejności po rodzicu, a następnie po jego synach, czyli zaczynamy od korzenia (element „F”), a następnie trafiamy do pierwszego syna po lewej stronie (element „B”), który to z kolei jest rodzicem dla elementu „A” oraz „D”, „D” z kolei jest rodzicem dla „C” i „E”. Tym sposobem przeszliśmy po całej lewej gałęzi i trafiamy do prawej czyli drugiego dziecka elementu „F” – „G”….
Kolejno wygląda to tak: F, B, A, D, C, E, G, I, H.
In-order
„Przejście poprzeczne” – zaczynamy od elementu najbardziej wysuniętego w lewo czyli elementu najmniejszego w danym drzewie, w naszym przykładzie „A”, następnie odczytujemy jego rodzica (element „B”) i kolejne dziecko, czyli znowu najbardziej wysunięty w lewo element „C”, dalej rodzica (element „D”) i dziecko – element „E”… kolejno mamy rodzica „F” oraz idziemy na lewo z „G” – jak widać nie ma takiego elementu więc przechodzimy do kolejnego kroku, elementu „G”…
Kolejno wygląda to tak: A, B, C, D, E, F, G, H, I.
Post-order
W przypadku porządku „Post-order” działanie wykonujemy na wszystkich synach, a następnie przechodzimy do ich rodziców. Czyli w naszym przykładzie odczytujemy element „A”, „C”, „E”, a następnie przechodzimy do rodzica „D”, „B” i dalej znowu dzieci „H” i rodzic „I” oraz „G”, a na końcu korzeń czyli „F”.
Kolejno wygląda to tak: A, C, E, D, B, H, I, G, F.


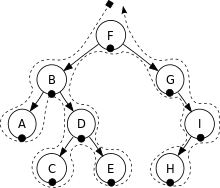

There is a mistake in an explenation of the In-order traversal of the BST tree. The IN-Order traversal of BST should be: A, B, C, D, E, F, H, I G.
You are not right, in this case the in-order traversal of BST is: A, B, C, D, E, F, G, H, I.